https://doi.org/10.1140/epjs/s11734-024-01103-8
Regular Article
Closed form expressions for certain improper integrals of mathematical physics
Centre for High Energy Physics, Indian Institute of Science, 560012, Bangalore, Karnataka, India
Received:
27
October
2023
Accepted:
19
January
2024
Published online:
8
February
2024
We present new closed-form expressions for certain improper integrals of Mathematical Physics such as certain Ising, Box, and Associated integrals. The techniques we employ here include (a) the Method of Brackets and its modifications and suitable extensions to obtain the Mellin–Barnes representation. (b) The evaluation of the resulting Mellin–Barnes representations via the recently discovered Conic Hull method via the automated package MBConichulls.wl. Finally, the analytic continuations of these series solutions are then produced using the automated package Olsson.wl, based on the method of Olsson. Thus, combining all these recent advances allows for closed-form evaluation of the hitherto unknown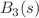 
, 
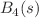and related integrals in terms of multi-variable hypergeometric functions. Along the way, we also discuss certain complications while using the Original Method of Brackets for these evaluations and how to rectify them. The interesting case of 
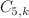is also studied. It is not yet fully resolved for the reasons we discuss in this paper.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to EDP Sciences, Springer-Verlag GmbH Germany, part of Springer Nature 2024. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
