https://doi.org/10.1140/epjs/s11734-025-01546-7
Regular Article
Mitigation of numerical asymmetries induced by Cartesian meshes with pseudo-spectral method in hydrodynamics simulations
1
College of Physics, Sichuan University, 610065, Chengdu, People’s Republic of China
2
Key Laboratory of High Energy Density Physics and Technology, Ministry of Education, Sichuan University, 610064, Chengdu, People’s Republic of China
a
ronghaohu@scu.edu.cn
b
lvmengphys@scu.edu.cn
Received:
18
December
2024
Accepted:
21
February
2025
Published online:
10
March
2025
Asymmetries play a vital role in the inertial confinement fusion experiments, which have been confirmed to reduce the fuel confinement and the energy coupling between shell kinetic energy and the hot spot internal energy. The Cartesian mesh-based hydrodynamics codes, commonly used in inertial confinement fusion simulations, are affected by numerical asymmetries in multi-dimensional simulations. The numerical asymmetries can result in incorrect growth rates of low-mode asymmetries seeded by physical perturbations that existed in targets, lasers and radiation drives. In this work, we introduce spectral methods with global approximation to the implosion and explosion simulations to attain fewer numerical asymmetries caused by local discretization. The spectral filtering technique is used to ensure numerical stability, and a new filter is presented to reduce the unphysical oscillations caused by the spectral approximation of discontinuous solutions. In one-dimensional simulations, the robustness and efficiency of this new filter are analyzed and compared with conventional ones in the presence of discontinuous solutions. The numerical asymmetries for the spectral and finite volume methods are quantitatively calculated in two-dimensional simulations of cylindrical explosions and implosions. The implosion simulation results reveal that numerical asymmetries for the spectral method can be below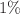 
for moderate spatial resolutions and even less than 
for high spatial resolutions, which are about one order of magnitude smaller than the finite volume method.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to EDP Sciences, Springer-Verlag GmbH Germany, part of Springer Nature 2025
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
