Eur. Phys. J. Spec. Top. (2021) 230: 3835-3844
https://doi.org/10.1140/epjs/s11734-021-00329-0

Regular Article

Multi-multifractality and dynamic scaling in stochastic porous lattice

Theoretical Physics Group, Department of Physics, University of Dhaka, 1000, Dhaka, Bangladesh

^b khassan@du.ac.bd

Received: 1 September 2021
Accepted: 30 October 2021
Published online: 20 November 2021

Abstract

In this article, we extend the idea of stochastic dyadic Cantor set to weighted planar stochastic lattice that leads to a stochastic porous lattice. The process starts with an initiator which we choose to be a square of unit area for convenience. We then define a generator that divides the initiator or one of the blocks, picked preferentially with respect to their areas, to divide it either horizontally or vertically into two rectangles of which one of them is removed with probability 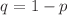$q=1-p$. 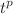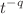We find that the remaining number of blocks and their mass varies with time as $t^p$ and $t^{-q}$, respectively. Analytical solution shows that the dynamics of this process is governed by infinitely many hidden conserved quantities each of which is a multifractal measure with porous structure as it contains missing blocks of various different sizes. The support where these measures are distributed is fractal with fractal dimension 2p provided 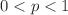$0<p<1$. We find that if the remaining blocks are characterized by their respective area, then the corresponding block size distribution function obeys dynamic scaling.