Eur. Phys. J. Spec. Top. (2022) 231: 1153-1158
https://doi.org/10.1140/epjs/s11734-022-00514-9

Regular Article

Approximate analytical solutions of the kinetic and balance equations for intense boiling

Laboratory of Multi-Scale Mathematical Modeling, Department of Theoretical and Mathematical Physics, Ural Federal University, Lenin ave., 51, 620000, Ekaterinburg, Russian Federation

^c dmitri.alexandrov@urfu.ru

Received: 3 March 2021
Accepted: 3 March 2022
Published online: 10 March 2022

Abstract

The process of intense boiling is theoretically studied on the basis of kinetic and balance equations for the bubble-size distribution function and system temperature. The kinetic equation for the bubble-size distribution function represents the first-order partial differential equation with a source term. The heat balance is spatially homogeneous and takes into account the heat exchange of the system with the external environment. This non-linear system is supplemented by the initial and boundary conditions. Namely, the initial bubble-size distribution and temperature are regarded as known, and the flux of bubbles overcoming the critical size is defined by the rate of nuclei formation. A non-linear integro-differential system of model equations is solved analytically by the integral Laplace transform and saddle-point methods. 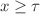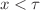It is shown that the solution has a different form at $x\ge \tau$ and $x<\tau$ (here, x and $\tau$ are the dimensionless spatial and temporal variables). Also, we show that the initial bell-shaped distribution function decreases, and the liquid temperature increases with increasing time.