https://doi.org/10.1140/epjs/s11734-023-00868-8
Review
An introduction to thermal field theory and some of its application
Theory Division, Saha Institute of Nuclear Physics, Homi Bhabha National Institute, 1/AF Bidhan Nagar, 700064, Kolkata, India
a
munshigolam.mustafa@saha.ac.in
Received:
15
February
2023
Accepted:
11
May
2023
Published online:
24
July
2023
In this article an introduction to the thermal field theory within imaginary time vis-a-vis Matsubara formalism has been discussed in detail. The imaginary time formalism has been introduced through both the operatorial and the functional integration method. The prescription to perform frequency sum for boson and fermion has been discussed in detail. Green’s function both in Minkowski time as well as in Euclidean time has been derived. The tadpole diagram in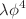 
theory and the self-energy in 
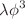theory have been computed and their consequences have also been discussed. The basic features of general two point functions, such as self-energy and propagator, for both fermions and bosons in presence of a heat bath have been discussed. The imaginary time has also been introduced from the relation between the functional integral and the partition function. Then the free partition functions and thermodynamic quantities for scalar, fermion and gauge field, and interacting scalar field have been obtained from first principle calculation. The quantum electrodynamics (QED) and gauge fixing have been discussed in details. The one-loop self-energy for electron and photon in QED have been obtained in hard thermal loop (HTL) approximation. The dispersion properties and collective excitations of both electron and photon in a material medium in presence of a heat bath have been presented. The spectral representation of fermion and gauge boson propagators have been obtained. In HTL approximation, the generalisation of QED results of two point functions to quantum chromodynamics (QCD) have been outlined that mostly involve group theoretical factors. Therefore, one learns about the collective excitations in a QCD plasma from the acquired knowledge of QED plasma excitations. Then, some subtleties of finite temperature field theory have been outlined. As an effective field theory approach the HTL resummation and the HTL perturbation theory (HTLpt) have been introduced. The leading order (LO), next-to-leading order (NLO) and next-to-next-leading order (NNLO) free energy and pressure for deconfined QCD medium created in heavy-ion collisions have been computed within HTLpt. The general features of the deconfined QCD medium have also been outlined with non-perturbative effects like gluon condensate and Gribov–Zwanziger action. The dilepton production rates from quark–gluon plasma with these non-perturbative effects have been computed and discussed in details.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to EDP Sciences, Springer-Verlag GmbH Germany, part of Springer Nature 2023. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
