https://doi.org/10.1140/epjs/s11734-023-01042-w
Regular Article
Patterns in bifurcation levels of the integral manifolds of the N body problem
1
Department of Computer Science, Northern Illinois University, 60115, DeKalb, IL, USA
2
Department of Mathematical Sciences, Northern Illinois University, 60115, DeKalb, IL, USA
Received:
28
April
2023
Accepted:
14
November
2023
Published online:
11
December
2023
In the N-body problem, it is classical that there are conserved quantities of center of mass, linear momentum, angular momentum, and energy. The level sets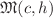 
of these conserved quantities are parameterized by the angular momentum c and the energy h, and are known as the integral manifolds. A long-standing goal has been to identify the bifurcation values, especially the bifurcation values of energy for fixed non-zero angular momentum, and to describe the integral manifolds at the regular values. Alain Albouy identified two categories of singular values of energy: those corresponding to relative equilibria, referred to as “finite bifurcations”; and those corresponding to “bifurcations at infinity”, and provided an algorithm for identifying all possible values of each. This requires identifying all central configurations for the N bodies and all sub-collections of the bodies. Using available data on central configurations for 10 or fewer equal masses, we apply Albouy’s analysis to enumerate all singular values, and study the patterns of “finite” vs. “infinite” bifurcations. In particular, we show that the conjecture that all bifurcations at infinity occur at energy levels less in magnitude than the finite bifurcations is false.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to EDP Sciences, Springer-Verlag GmbH Germany, part of Springer Nature 2023. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
