https://doi.org/10.1140/epjs/s11734-023-00850-4
Review
Kronecker coefficients from algebras of bi-partite ribbon graphs
1
Laboratoire d’Informatique de Paris Nord UMR CNRS 7030, Université Paris 13, 99 avenue J.-B. Clement, 93430, Paris, Villetaneuse, France
2
School of Physical and Chemical Sciences, Queen Mary University of London, Mile End Road, E14 6HT, London, United Kingdom
3
International Chair in Mathematical Physics and Applications, ICMPA–UNESCO Chair, 072 B.P. 50, Cotonou, Benin
4
School of Physics and Mandelstam Institute for Theoretical Physics, University of Witwatersrand, Wits 2050, Johannesburg, South Africa
Received:
1
November
2022
Accepted:
25
April
2023
Published online:
26
May
2023
Bi-partite ribbon graphs arise in organizing the large N expansion of correlators in random matrix models and in the enumeration of observables in random tensor models. There is an algebra 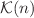 , with basis given by bi-partite ribbon graphs with n edges, which is useful in the applications to matrix and tensor models. The algebra
, with basis given by bi-partite ribbon graphs with n edges, which is useful in the applications to matrix and tensor models. The algebra 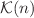 is closely related to symmetric group algebras and has a matrix-block decomposition related to Clebsch–Gordan multiplicities, also known as Kronecker coefficients, for symmetric group representations. Quantum mechanical models which use
is closely related to symmetric group algebras and has a matrix-block decomposition related to Clebsch–Gordan multiplicities, also known as Kronecker coefficients, for symmetric group representations. Quantum mechanical models which use 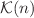 as Hilbert spaces can be used to give combinatorial algorithms for computing the Kronecker coefficients.
as Hilbert spaces can be used to give combinatorial algorithms for computing the Kronecker coefficients.
Joseph Ben Geloun and Sanjaye Ramgoolam have contributed equally to this work.
S.I.: Noncommutativity and Physics. Guest editors: George Zoupanos, Konstantinos Anagnostopoulos, and Peter Schupp.
© The Author(s) 2023
 Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.





