https://doi.org/10.1140/epjs/s11734-023-01070-6
Regular Article
Triangular tessellations of one-loop scattering amplitudes in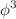 
theory
Centre for High Energy Physics, Indian Institute of Science, 560012, Bangalore, Karnataka, India
a abhijit@iisc.ac.in, abhijitdas123654@gmail.com
Received:
12
October
2023
Accepted:
7
December
2023
Published online:
24
January
2024
Inspired by the recent work of Nima Arkani Hamed and collaborators who introduced the notion of positive geometry to account for the structure of tree-level scattering amplitudes in bi-adjoint 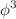theory, which led to one-loop descriptions of the integrands. Here, we consider the one-loop integrals themselves in 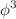theory. In order to achieve this end, the geometrical construction offered by Schnetz for Feynman diagrams is hereby extended, and the results are presented. The extension relies on masking the loop momentum variable with a constant and proceeding with the calculations. The results appear as a construction given in a diagrammatic manner. The significance of the resulting triangular diagrams is that they have a common side amongst themselves for the corresponding Feynman diagrams they pertain to. Further extensions to this mathematical construction can lead to additional insights into higher loops. A mathematica code has been provided in order to generate the final results given the initial parameters of the theory.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to EDP Sciences, Springer-Verlag GmbH Germany, part of Springer Nature 2024. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
