https://doi.org/10.1140/epjs/s11734-024-01346-5
Regular Article
Impact of surveillance in human-to-human transmission of monkeypox virus
1
Department of Mathematics, Federal University Dutse, 7156, Jigawa, Nigeria
2
Department of Mathematics, Prime University, Abuja, Nigeria
3
Department of Computer Engineering, Biruni University, Istanbul, Turkey
4
Department of Computer Science and Mathematics, Lebanese American University, P.O. Box 13-5053, Beirut, Lebanon
5
Department of Mathematics, Near East University, 99138, Mersin, Turkey
6
Department of Medicine, University of Maiduguri, 1069, Maiduguri, Nigeria
7
Department of Medicine, Yobe State University, 1144, Damaturu, Yobe State, Nigeria
8
Faculty of Engineering and Natural Sciences, Istanbul Okan University, Istanbul, Turkey
9
Faculty of Engineering and Natural Sciences, Bahcesehir University, Istanbul, Turkey
Received:
10
July
2024
Accepted:
16
September
2024
Published online:
18
October
2024
Monkeypox has become the major orthopoxvirus causing infection since the eradication of smallpox 1980s. In this paper, we developed a compartmental mathematical model that describes the transmission dynamics of the monkeypox virus incorporating contact tracing (surveillance), pre-exposure, and post-exposure vaccination. It is shown that the model is mathematically well posed and can be used to study, predict, and make suggestions on the transmission and control of the monkeypox virus. The qualitative analysis of the model shows that the model exhibits two equilibrium states: monkeypox-free and endemic equilibriums. In addition to these equilibria, the model undergoes backward bifurcation. The effective reproduction number (control parameter) is determined and the stability of two equilibriums is established using the calculated reproduction number. The monkeypox-free equilibrium is locally and globally asymptotically stable when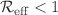 
. The endemic equilibrium on the contrary exists if 
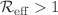and there is a small or negligible number of vaccinated individuals (about 
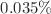of the population) per week. The endemic equilibrium is globally stable under certain conditions. Model fitting and parameter estimations are performed using the least-squares curve fittings. The simulation result of the model shows that in the absence of disease surveillance, the number of un-traced infectious individuals will grow and this can lead to a large number of new infections that may lead to the outbreak of the disease. However, to avoid the outbreak, the model incorporated isolation of those un-traced infectious individuals who show symptoms of the disease. The result also shows that contact tracing, disease surveillance isolation, and vaccination can entirely stall human–human monkeypox virus transmission.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to EDP Sciences, Springer-Verlag GmbH Germany, part of Springer Nature 2024
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
