https://doi.org/10.1140/epjs/s11734-024-01246-8
Regular Article
Modeling of COVID-19 with vaccination and optimal control
Department of Mathematics, School of Advanced Sciences, Vellore Institute of Technology, 600 127, Chennai, Tamil Nadu, India
Received:
13
April
2024
Accepted:
5
July
2024
Published online:
16
July
2024
COVID-19 is a respiratory disease caused by the virus SARS-CoV-2. As of now, millions of people have died as a result of the devastating COVID-19 outbreak. Vaccination can lessen the severity of COVID-19, even though there is no known cure for it. Here, we propose and develop a novel COVID-19 epidemiological vaccination model. Then, we find the disease-free and endemic equilibria for our proposed model and compute the basic reproduction number (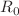
). We discuss the sensitivity analysis to visualize the impact of different parameters mainly associated with vaccination. Through numerical simulation, it has been shown that increasing treatment and vaccination rates reduces the transmission and increases the recovery, respectively. By taking into account two control parameters—namely, those related to the disease’s rate of diagnosis and transmission—the suggested model is extended to an optimal control problem. It has been observed that both control parameters have a significant impact on limiting the spread of COVID-19. The main goal of this study is to find out how vaccination, when compared to no vaccination, can reduce the spread of disease.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to EDP Sciences, Springer-Verlag GmbH Germany, part of Springer Nature 2024. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
