https://doi.org/10.1140/epjs/s11734-025-01552-9
Regular Article
Fractal dimensions of the dispersive wave equation
1
School of Mathematics, Northwest University, 710127, Xi’an, Shaanxi, People’s Republic of China
2
Shaanxi Key Laboratory of Mathematical Theory and Computation of Fluid Mechanics, School of Mathematics, Northwest University, 710127, Xi’an, Shaanxi, People’s Republic of China
3
Analysis, Probability and Fractals Laboratory LR18ES17, Department of Mathematics, Faculty of Sciences of Monastir, University of Monastir, 5000, Monastir, Tunisia
Received:
24
August
2024
Accepted:
28
February
2025
Published online:
14
March
2025
In this paper, we primarily investigate fractal solutions to the dispersive wave equation. We prove a series of fractal propositions related to this equation and determine various fractal dimensions, including Box dimension, Hausdorff dimension, Packing dimension,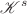 
-dimension, and 
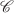-dimension. Additionally, we present some fractal dimensions for the fractal solutions of the dispersive wave equation. These findings will contribute to developing a computational framework for fractal dimensions in certain differential equations.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to EDP Sciences, Springer-Verlag GmbH Germany, part of Springer Nature 2025
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
