https://doi.org/10.1140/epjs/s11734-025-01705-w
Regular Article
On the multilayer neural networks for analyzing the (1 + 1)-dimensional space-time fractional equation for Granular model
1
Department of Mathematics, Cooch Behar Panchanan Barma University, 736101, Cooch Behar, India
2
Department of Mathematics, Mathabhanga College, 736146, Cooch Behar, India
3
Department of Mathematical Sciences, College of Science, Princess Nourah bint Abdulrahman University, P.O. Box 84428, 11671, Riyadh, Saudi Arabia
4
Mathematics Department, Faculty of Science, University of Tabuk, Tabuk, Saudi Arabia
5
Department of Physics, Faculty of Science, Port Said University, 42521, Port Said, Egypt
6
Department of Physics, Faculty of Science, Al-Baha University, P. O. Box 1988, Al-Baha, Saudi Arabia
a tantawy@sci.psu.edu.eg, samireltantawy@yahoo.com
Received:
4
April
2025
Accepted:
19
May
2025
Published online:
3
June
2025
This article uses multilayer neural networks to solve the (1 + 1)-dimensional space-time fractional equation for the Granular model. The investigation occurs two-fold: First, the integrability of the said model equation is confirmed through fractional Lax pairs, bilinear structure, and multi-shock solutions. Second, by choosing the appropriate activation functions and neuron coefficients based on the fractional bilinear form, a range of significant solutions encompassing breather, lump, and shock waves are derived. To achieve interaction solutions, a novel test function approach is considered that integrates a quadratic function, a bi-exponential function, and a cosine function. At patterns “2-3-1”, “2-4-1”, and “2-2-2-1”, the interactions between lump type, periodic kink, and two-shock-like waves and periodic lump-kink waves are built where absorption, escape, and reabsorption of wave structures are found. Some two and three-dimensional graphs have been exhibited to highlight the features and significant effects of fractional order (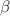
) in the solutions.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to EDP Sciences, Springer-Verlag GmbH Germany, part of Springer Nature 2025
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
