https://doi.org/10.1140/epjs/s11734-021-00313-8
Regular Article
On the topological Billingsley dimension of self-similar Sierpiński carpet
1
Algebra, Number Theory and Nonlinear Analysis Laboratory, LR18ES15, Department of Mathematics, Faculty of Sciences of Monastir, University of Monastir, Monastir, Tunisia
2
Department of Mathematics, Higher Institute of Applied Mathematics and Computer Sciences, University of Kairouan, Street of Assad Ibn Alfourat, 3100, Kairouan, Tunisia
3
Department of Mathematics, Faculty of Sciences, University of Tabuk, Tabuk, Saudi Arabia
4
Analysis, Probability and Fractals Laboratory LR18ES17, Department of Mathematics, Faculty of Sciences of Monastir, University of Monastir, 5000, Monastir, Tunisia
b bilel.selmi@fsm.rnu.tn, bilel.selmi@isetgb.rnu.tn
Received:
17
May
2021
Accepted:
25
October
2021
Published online:
10
November
2021
In studying physical systems, it is usually convenient to consider their dimensions. In the classical sense, this turns around the dimension of the Euclidean space where the variables live. Next, with the discovery of non-Euclidean geometry, hidden structures, and with the technological developments, the concept of dimension have been extended to fractal cases such as Billingsley and topological ones and which are also kinds of invariants permitting to describe the irregularity hidden in irregular objects via growth laws. In the present paper, the main purpose was to extend the concept of fractal dimension by introducing a variant of the Billingsley dimension called the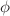 
-topological Billingsley dimension, relative to a non-negative function 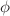defined on a collection of subsets of a metric space. Some connections with the topological and Hausdorff dimensions have been also discussed on the basis of the well-known self-similar Sierpiński carpet. Besides, a class of functions has been provided, for which the computation of the new dimension is possible, and where the equality holds for the upper and lower bounds of the 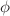-topological Billingsley dimension.
© The Author(s), under exclusive licence to EDP Sciences, Springer-Verlag GmbH Germany, part of Springer Nature 2021
