https://doi.org/10.1140/epjs/s11734-021-00337-0
Regular Article
Approximation by non-self-referential bivariable fractal functions
1
Department of Mathematics, Visvesvaraya National Institute of Technology, Nagpur, India
2
Department of Computer Science and Biomedical Informatics, University of Thessaly, Lamia, Greece
Received:
23
July
2021
Accepted:
30
October
2021
Published online:
22
November
2021
Fractal functions defined through iterated function systems provide a new technique for the approximation of functions. Non-self-referential bivariable fractal functions which approximate a given continuous function defined on a rectangle in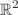 
are developed herein. Moreover, by imposing suitable conditions on the scaling factors and on base functions, we study 
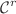-non-self-referential bivariable fractal functions.
© The Author(s), under exclusive licence to EDP Sciences, Springer-Verlag GmbH Germany, part of Springer Nature 2021
