https://doi.org/10.1140/epjs/s11734-023-00841-5
Review
Generalized symmetries as homotopy Lie algebras
1
Division of Theoretical Physics, Rudjer Bošković Institute, Bijenička 54, 1000, Zagreb, Croatia
2
School of Theoretical Physics, Dublin Institute for Advanced Studies, 10 Burlington Road, Dublin 4, Ireland
Received:
1
August
2022
Accepted:
14
April
2023
Published online:
26
April
2023
Homotopy Lie algebras are a generalization of differential graded Lie algebras encoding both the kinematics and dynamics of a given field theory. Focusing on kinematics, we show that these algebras provide a natural framework for the description of generalized gauge symmetries using two specific examples. The first example deals with the non-commutative gauge symmetry obtained using Drinfel’d twist of the symmetry Hopf algebra. The homotopy Lie algebra compatible with the twisted gauge symmetry turns out to be the recently proposed braided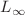 
-algebra. In the second example, we focus on the generalized gauge symmetry of the double field theory. The symmetry includes both diffeomorphisms and gauge transformation and can consistently be defined using a curved 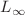-algebra.
S.I.: Noncommutativity and Physics. Guest editors: George Zoupanos, Konstantinos Anagnostopoulos, Peter Schupp.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to EDP Sciences, Springer-Verlag GmbH Germany, part of Springer Nature 2023. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
