https://doi.org/10.1140/epjs/s11734-025-01520-3
Regular Article
Simulating rotating newtonian universes
1
Department of Physics of Complex Systems, ELTE Eötvös Loránd University, Budapest, Hungary
2
Institute for Particle and Nuclear Physics, HUN-REN Wigner Research Centre for Physics, Budapest, Hungary
3
Institute for Astronomy, University of Hawai’I at Mānoa, Honolulu, HI, USA
4
Department of Physics, University of Helsinki, Helsinki, Finland
Received:
15
October
2024
Accepted:
7
February
2025
Published online:
27
February
2025
We present the results of a novel type of numerical simulation that realizes a rotating Universe with a shear-free, rigid body rotation inspired by a Gödel-like metric. We run cosmological simulations of unperturbed glasses with various degrees of rotation in the Einstein–de Sitter and the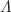 
CDM cosmologies. To achieve this, we use the StePS N-body code capable of simulating the infinite Universe, overcoming the technical obstacles of classical toroidal (periodic) topologies that would otherwise prevent us from running such simulations. Results show a clear anisotropy between the polar and equatorial expansion rates with more than 
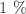deviation from the isotropic case for maximal rotation without closed timeline curves within the horizon,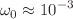 
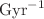; a considerable effect in the era of precision cosmology.
© The Author(s) 2025
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
